ma412: Abstract Algebra II - w25

(CC BY-SA 4.0) : author(s): David Moore, Stephen Brooks
(CC BY-SA 4.0) : link
Class Meetings
- Winter 2025 (Jan13 → May3)
- MWF 10:00-10:50AM
- TFA 233
- zoom link - passcode 077600
Instructor

Daniel Rowe
darowe{at}nmu{dot}edu
I'm an associate professor of mathematics in the Mathematics and Computer Science Department at Northern Michgan University. I've been a professor at NMU for nine years, and I am very passionate about the praxis of doing mathematics and teaching it. I grew up on a fishing camp in Northwestern Ontario, Canada.
Need Math Help?
- Office Hours
- W 1-2, R 11-12, F 11-12
- JXJ 2228
- zoom link - passcode 809390
- read the relevant section(s) of our materials
- study all posted solutions
- re-watch the recorded lectures
- math tutor lab
Class Structure
- hybrid-flexible, in-person and over zoom
- recordings available 2-3 days after each class
- strive for in-person attendance
- avoid becoming reliant on zoom and recordings!
- use them for extenuating circumstances only
- engagement is vital to learning mathematics (or anything)
- (40%) Homework
- (30%) Traditional In-Class Midterm Exam
- (30%) Traditional In-Class Final Exam
Grade Scale
A (92-100%)
A- (90-91%)
B+ (86-89%)
B (82-85%)
B- (80-81%)
C+ (76-79%)
C (72-75%)
C- (70-71%)
D+ (66-69%)
D (62-65%)
D- (60-61%)
F (≤ 59%)
Learning Outcomes
This course is a continuation of ma312: Abstract Algebra I.
With an understanding of the theory of groups in hand, this semester will focus on the study of rings and fields. The eventual goal is Galois theory, which is a beautiful interaction between the concepts of groups, rings, and fields. By the end of the class, students will be comfortable making calculations with, and applying:
finite abelian groups
Euler's formula
polynomial rings, rational function fields
Gaussian integers and Gaussian primes
irreducible polynomials over the integers
symmetric functions
Galois theory
Success in College Courses
- the instructor's job is to ensure the course content is clear, organized, and interesting
- your job is to attend as many classes as you can, engage your mind, ask questions, read, and budget (at least) 1-2 focused hours every week
to work on the course content
Academic Honesty
In the spirit of academic honesty, credit for this section is due to Asher Auel, as this is an adapted form of their discussion of academic honesty in mathematics.
- Working with others on mathematics, and using electronic resources is both highly encouraged and fun. You may work with anyone (e.g. classmates, non-classmates, tutors, etc.) If this is done well, you'll learn more effectively and efficiently.
Here's the fundamental rule:
Work with anyone or anything to develop your own personal understanding of the ideas required to solve your homework problem, but always write-up the final draft by yourself and in your own words.
- Writing up the final draft is just as important as figuring out the problems on scratch paper with your friends, using the internet, ChatGPT, etc. If you work with people, or use electronic resources on a particular homework:
You must list your collaborators and electronic sources at the top of the very first page. This makes the process completely transparent and honest.
A Note About Copying Mathematics
Mathematical writing is idiosyncratic; if your assignments are copied, it is quite easy to tell. You will not learn by copying solutions from others, or from external sources such as internet forums (e.g. math.stackexchange) and generative AI (e.g. ChatGPT). Regarding internet forums, you are free to look at them and use any understanding you've gained from them. Be warned that internet forums often contain incorrect or circuitous solutions, misleading discussions, use of techniques outside of the course material, and other material that may be detrimental to your learning process. Even the time that it takes to repeatedly search for solutions and read through dozens of forum posts could be better spent learning the material on your own or composing a question to the instructor or classmate. Regarding generative AI (e.g. ChatGPT), you are free to experiment with asking questions, but be warned that these systems are currently still very bad at deductive reasoning, and that the output may contain a mix of correct, incorrect, and unverified statements. Ask them to prove something false, they will work hard to do so, often giving contradictory answers. Therefore, I would be very careful with using these tools as learning resources on your own.
Punishments
In this modern world of online resources, cheating, copying, copy-and-pasting, ChatGPT, etc.; it is now more important than ever that citizens develop the intelligence to use their own brain to solve problems. I want my classes to be a postive force in this regard, by promoting the principles of academic honesty, and punishing those who disrespect those principles. The first infraction will result in a 0% on the entire assigment and a stern warning. If there is a second infraction, I will pursue sanctions through the Dean of Students office.
Accessibility
If you have a need for disability-related accommodations or services, please inform the Coordinators of Disability Services in the Dean of Students Office at 2001 C. B. Hedgcock Building (227-1737 or disability@nmu.edu). Reasonable and effective accommodations and services will be provided to students if requests are made in a timely manner, with appropriate documentation, in accordance with federal, state, and University guidelines.
Reading Materials
- Here are my hand-written notes on abstract algebra II.
- The following is a decent, free, open textbook:
- How do I read the text to follow the flow of our class?
- 6 → 13 → 16 → 17 → 18 → 21 → 22 → 23
- for review, here are my notes on abstract algebra I
Homework + Quizzes + Exams + Extra Credit
- hw1 → sol (posted 2/4 @ 10:30am)
- hw2 → sol (posted 2/13 @ 3:20pm)
- hw3 → sol (posted 2/25 @ 12:30pm)
- hw4 → sol (posted 3/18 @ 2:20pm)
- hw5 → sol (posted 4/16 @ 2:20pm)
- hw6 → sol (posted 4/29 @ 1:00PM)
- practice midterm → sol
- midterm_exam → sol
- practice final → sol
- final_exam
- extra credit problems
- list of extra credit problems
- (please read the instructions before you submit)
- repository of solved extra credit problems
- (check which problems have been solved already!)
Submitting Your Work
- for quizzes, midterm, final: physical paper in-class
- for extra credit: email me a .pdf (read instructions in the link above)
- for homework: put a .pdf file inside our shared google folder
- the shared google folder will be titled w25_ma412_yourlastname
- I will share it with you within first two weeks of class
- please don't submit anything via email attachment
- name your files in an organized manner, for example: hw1_Jane_Smith.pdf
- always show your work and keep it organized
- indicate/circle/highlight your answers
- answer the questions in the correct order
Late Submissions
- for quizzes, midterm, final: submitted in class on the day
- for homework submissions: no late penalty until
the solutions are posted, then -50%
Checking Your Grade
- you can check your grade anytime, look for
untitled spreadsheet in our shared folder,
it will appear after the first few assignments
have been graded
Schedule + Recordings
> colored text = clickable links
> late homework may be submitted anytime during the semester
> before the solutions are posted (-0%), otherwise (-50%)
wk1: jan13 → jan17
□ study this webpage and all class information
□ study the lectures
□ start working on hw1
- 1/13
- class overview
- review of abstract algebra I
- tour of abstract algebra II
- 1/15
- Evariste Galois
- symmetries of roots of polynomials
- 1/17
- finite Abelian groups and Z-lattices
wk2: jan20 → jan24
□ study the lectures
□ keep working on hw1
- 1/22
- the relationship to Z-matrices
- GLn(Z)-row and column operations
- algorithm for reducing Z-matrices
- 1/24
- structure theorem of finite Abelian groups
- help with hw1
wk3: jan27 → jan31
□ study the lectures
□ finish up hw1
□ start working on hw2
- 1/27
- more help with hw1
- invariant factors/elementary divisors
- 1/29
- the complex numbers
- Euler's formula
wk4: feb3 → feb7
□ study the lectures
□ keep working on hw2
- 2/3
- example of complex roots of x^n-1=0
- polynomial systems
- the example of Z[1/5]
- 2/5
- FIRST HALF OF RECORDING IS MA211 - sorry!
- polynomial systems
- the example of Z[1/5]
- the example of Z[sqrt(2)]
- 2/7
- help with hw2
- the definition of a "ring"
wk5: feb10 → feb14
□ study the lectures
□ start working on hw3
- 2/10
- the definition of a "ring"
- rings and polynomials
- the group of units of a ring
- 2/12
- more examples of unit groups
- 2/14
- rational function fields
- the phenomenon of Q[a]=Q(a)
wk6: feb17 → feb21
□ study the lectures
□ keep working on hw3
- 2/17
- fields
- polynomial division
- reduced expressions in Q[a]
- 2/21
- help with hw3
- ring homomorphisms
wk7: feb24 → feb28
□ study the lectures
□ start working on hw4
- 2/24
- help with hw4
- more ring homomorphisms
- 2/28
- no class - rowe travelling
wk8: mar10 → mar14
□ study the lectures
□ keep working on hw4
□ study for midterm exam next wed
- 3/10
- kernels and ideals
- factoring in rings
wk9: mar17 → mar21
□ study the lectures
□ midterm exam on wednesday
□ start working on hw5
- 3/21
- p=a2+b2 exactly when p=2 or p=4k+1
- when is an arbitrary integer the sum of two squares?
wk10: mar24 → mar28
□ study the lectures
□ keep working on hw5
- 3/24
- field extensions of Q (number fields)
wk11: mar31 → apr4
□ study the lectures
□ keep working on hw5
- 4/2
- cyclotomic fields
- splitting fields
wk12: apr7 → apr11
□ study the lectures
□ finish up hw5
- 4/7
- Galois groups of cyclotomic polys
- 4/9
- another Galois group example
- help with hw5
- 4/11
- help with hw5
- symmetric functions
- elementary symmetric functions
wk13: apr14 → apr18
□ study the lectures
□ start working on hw6
- 4/14
- recording first half: ma211
- recording second half: ma412
- discriminants and A3 versus S3
- 4/16
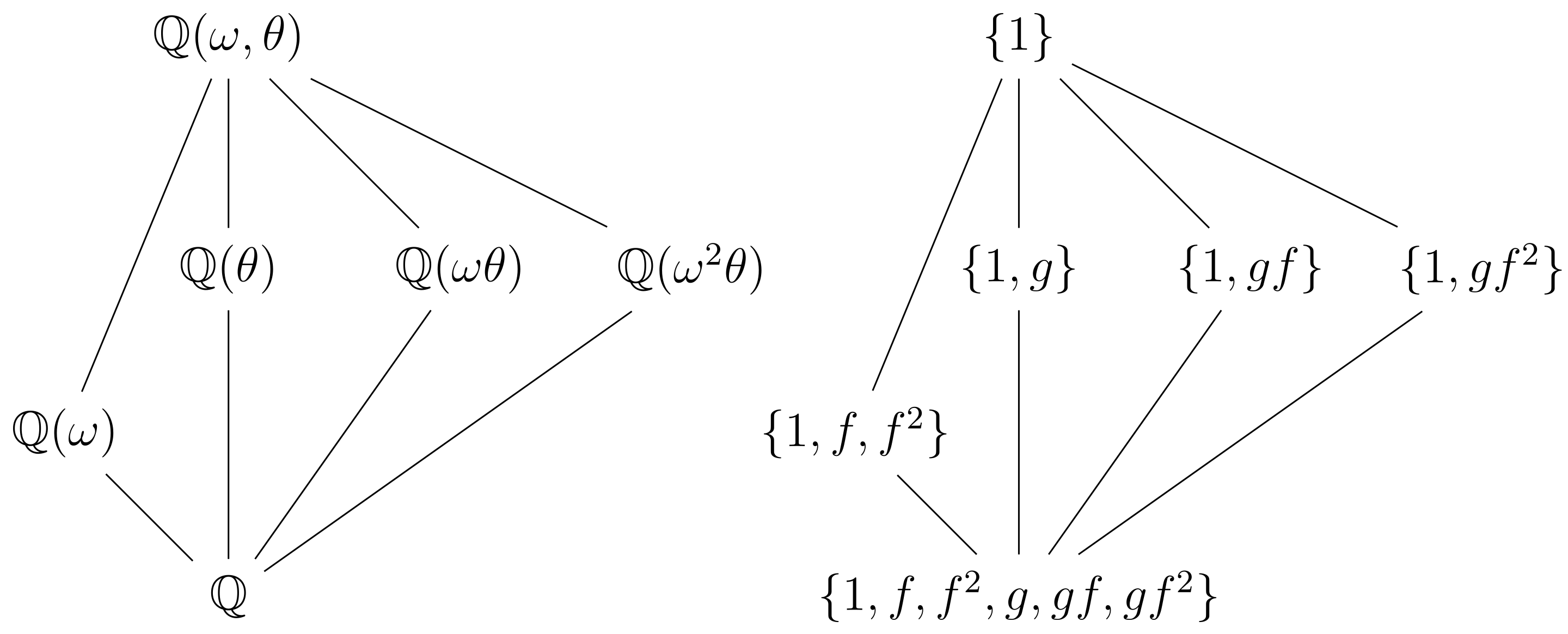
- the Galois correspondence
- examples
- 4/18
- the Galois correspondence
- examples
- two videos about Galois' ideas:
- (1) insolvability of the quintic
- (2) interesting problem connected to Φ5
wk14: apr21 → apr25
□ study the lectures
□ finish up hw6
- 4/21
- help with hw6
- the Galois correspondence
- examples
wk15: apr28 → may2 (FINAL EXAM WEEK)
□ final exam date: Mon 4/28 @ 10am
□ traditional in-person exam
□ no electronic devices
□ complete any late homework for 50%
□ deadline for extra credit and late homeworks
□ Thursday 5/1 @ 11:59PM


