Sky Diving and the Exponential Function

A sky diver jumps from a high altitude and falls to the earth experiencing air resistance proportional to her velocity, where we assume the constant of proportionality is 0.2. Let's take Stewart's word that the downward velocity of the diver at at time t seconds is 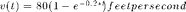$v(t) = 80(1-e^{-0.2*t})$ .

The velocity function
What's the initial velocity?
What's the velocity after 5 seconds? 10 seconds?
A graph of the velocity function
The maximum velocity of a falling object is its terminal velocity.
The Position of the Skydiver is
Initial Height
Plot the height over time

The velocity function

	k = -0.051;
	t = 0:60*5;
	T = -900;
	v = @(t) T * (1-exp(k.*t)); %Terminal velocity = 614 m/h = 900 ft/s

What's the initial velocity?

	InitialVelocity = v(0)

InitialVelocity =

     0

What's the velocity after 5 seconds? 10 seconds?

	AfterFiveSeconds = v(5)
	AfterTenSeconds  = v(10)

AfterFiveSeconds =

 -202.5752


AfterTenSeconds =

 -359.5540

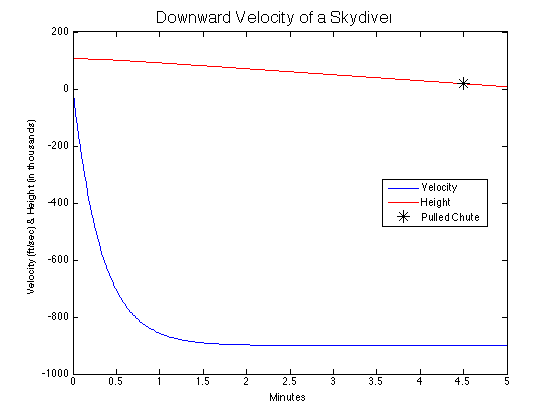
A graph of the velocity function

	plot(t/60,v(t));
	hold on;
	xlabel('Minutes');
	ylabel('Velocity (ft/sec) & Height (in thousands)');
	title('\fontsize{16}Downward Velocity of a Skydiver');

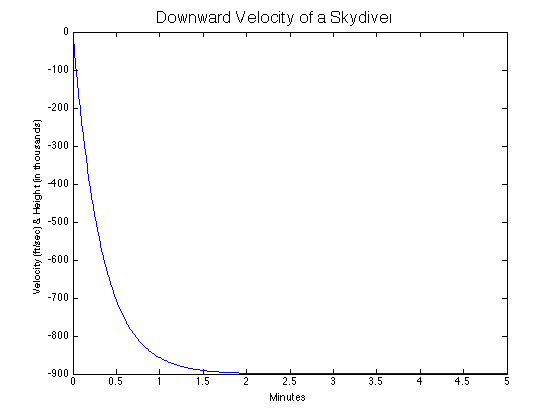
The maximum velocity of a falling object is its terminal velocity.

Can you find the terminal velocity from the graph?

The Position of the Skydiver is

	h = @(t) (-900 + 550)*(t-1/k*exp(k.*t)) + 113000;

Initial Height

	InitialHeight = h(0)

InitialHeight =

   1.0614e+05

Plot the height over time

	FreeFallTime = 4.5
	PullHeight = h(FreeFallTime*60);
	plot(t/60,h(t)/1000,'-r')
	plot(FreeFallTime,h((FreeFallTime)*60)/1000,'*k','MarkerSize',12);
	legend('Velocity','Height','Pulled Chute','Location','Best')

FreeFallTime =

    4.5000