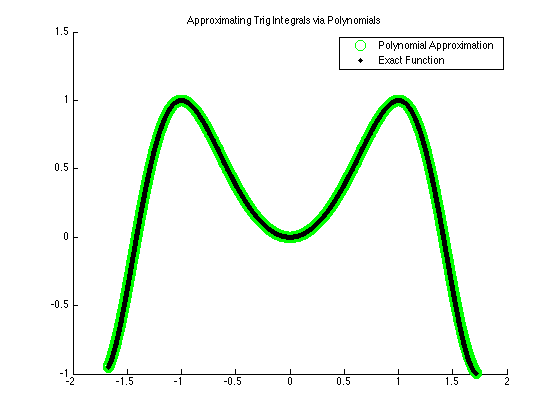
Compare the integrals of an approximating function and the standard one

This script requires ExT6_2point3 to be run prior

Contents

Define a vector of x-values and evaluate the polynomial s at these values

x = [min(x_given):.001:max(x_given)];
y = eval(s);

Compute the integral of the polynomial numerically

Integral_Approx = trapz(x,y)

Integral_Approx =

    1.1127

Compute the integral of the trig function numerically

For T6

Integral_Exact = trapz(x,sin( (pi*x.^2)/2 ))
% For T7
%Integral_Exact = trapz(x,exp(x.^2))

Integral_Exact =

    1.1048

Compute the difference between the two integrals

Defect = abs(Integral_Approx - Integral_Exact)

Defect =

    0.0079

Plot the two curves and the area under the curve

Plot the poly in green

figure; hold on;
title('Approximating Trig Integrals via Polynomials')
plot(x,y,'og','MarkerSize',10)
pause
% Plot the sine curve in black
plot(x,sin( (pi*x.^2)/2 ),'.k','MarkerSize',10)
% For T7
%plot(x,exp(x.^2));

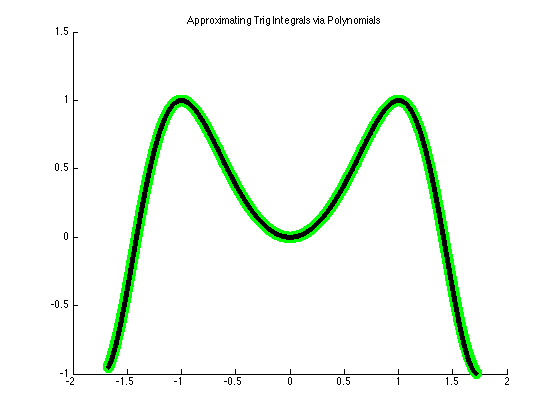
Create a legend

legend('Polynomial Approximation', 'Exact Function')

Published with MATLAB® 7.14