Find a polynomial of degree n that passes through the n+1 points
An Application of a Linear System
Contents
Define (x,y) pairs
P = [1,1; 2,3; 3,5; 4,-2; 5,11; 6,-12] % Define six (different) (x,y) pairs %P = [1,1; 2,4; 3,9; 4,16,; 5,25; 6,36];
P =
1 1
2 3
3 5
4 -2
5 11
6 -12
For each pair of points in P, create a line in an augemented matrix
representing a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4
A = [1 1 1 1 1 1 1; 1 2 4 8 16 32 3; 1 3 9 27 81 243 5; 1 4 16 64 4^4 4^5 -2; 1 5 25 125 5^4 5^5 11; 1 6 6^2 6^3 6^4 6^5 -12] % The augmented matrix for the alternate P %A = [1 1 1 1 1 1 1; % 1 2 4 8 16 32 4; % 1 3 9 27 81 243 9; % 1 4 16 64 4^4 4^5 16; % 1 5 25 125 5^4 5^5 25; % 1 6 6^2 6^3 6^4 6^5 36]
A =
Columns 1 through 6
1 1 1 1 1 1
1 2 4 8 16 32
1 3 9 27 81 243
1 4 16 64 256 1024
1 5 25 125 625 3125
1 6 36 216 1296 7776
Column 7
1
3
5
-2
11
-12
Compute the rref of A
M = rref(A);
% The last column of a are the coefficients of the polynomial
a = M(:,end)
a = 169.0000 -374.5161 295.0417 -104.4583 16.9583 -1.0250
To create a vector approximation to this polynomial
Create a vector of x-values between 0 and 7, counting by .01
x = 0:.01:7; y = a(1) + a(2)*x + a(3)*x.^2 + a(4)*x.^3 + a(5)*x.^4 + a(6)*x.^5;
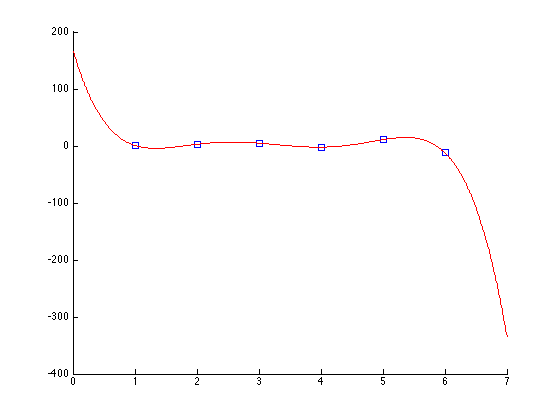
To plot the polynomial
figure; hold on; plot(P(:,1),P(:,2),'sb') pause plot(x,y,'r')