Using & Interpreting Linear Models

w/ggstats

Published

September 17, 2025

ggstats: cools stats package for ggplot

The ggstats package provides new statistics, new geometries and new positions for ggplot2 and a suite of functions to facilitate the creation of statistical plots.

  1. Install ggstats as shown below.
  2. You may need to update ggplot.
  3. Learn more here
library(ggplot)
install.packages("ggstats")
library(ggstats)

swiss dataset & the lm() function

The swiss dataset is a classic dataset of Fertility & Socioeconomic Indicators in Switzerland in 1888.

# skim the help file
?swiss

With the function lm() we fit a linear model to data. Specifically, we’ll use regression: Estimating the relationship between a dependent variable and one or more independent variables.

Below we predict the Fertility variable based on the other data in swiss (least squares regression). The coefficients of the model are contained in mod1 and can be used to determine the strength of our model.

# compute a least squares regression
mod1 <- lm(Fertility ~ ., data = swiss)

print(mod1)

Call:
lm(formula = Fertility ~ ., data = swiss)

Coefficients:
     (Intercept)       Agriculture       Examination         Education  
         66.9152           -0.1721           -0.2580           -0.8709  
        Catholic  Infant.Mortality  
          0.1041            1.0770

quick visualization of lm() output

The ggstats package allows for quick viewing of the coefficients.

Remember p-value < 0.05 ( 5 % ) usually means statistically significant. The Beta value on the x-axis represents the magnitude & direction between the variables, i.e., (+/- coorelation)

ggcoef_model(mod1, plot_title = "Predicting Fertility")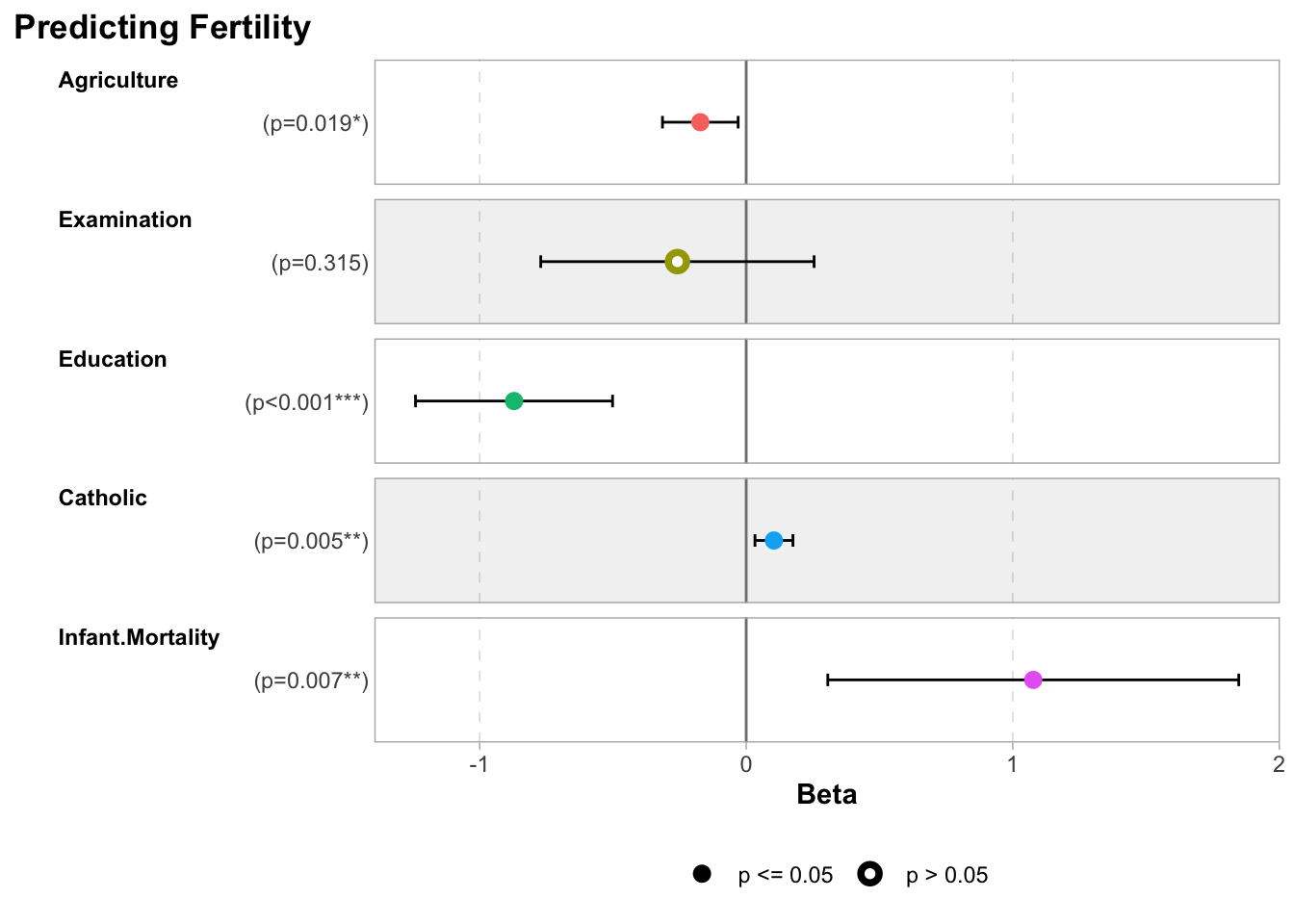

questions

  1. Based on the plot, what variable is most highly coorelated with Fertility?
  2. Which variable has no significant impact on Fertility?
  3. Apply these data-viz techniques to the penguins. You will have to select only the numeric variables first.
  4. Repeat but after you create a new variable called bill_ratio = bill_length_mm / bill_depth_mm